Optical resonators act as fundamental building blocks on laser systems. They determine crucial performance characteristics like beam quality, stability, and output power. Choosing between different resonator configurations impacts laser performance. Two main designs lead the field: Fabry - Perot (F - P) cavity and coaxial spherical cavity. Understanding their core differences matters for optimizing laser design and reliable operation.
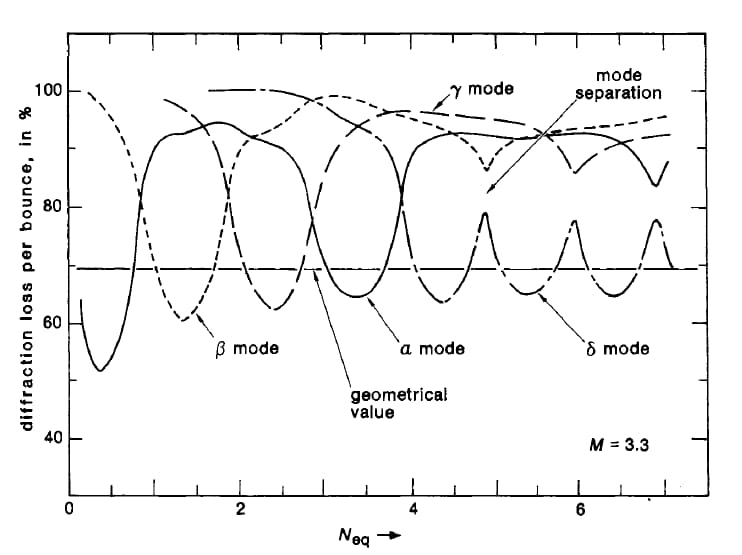
Modern optical resonators face multiple loss mechanisms limiting efficiency and stability. These losses fall into five types. Each type degrades system performance.
Transmission losses happen through cavity mirrors. Mirrors never reach perfect reflectivity.
Absorption and scattering losses come from light interacting with cavity’s working material.
Geometric deflection losses arise when light rays escape cavity boundaries due to geometry.
Diffraction losses occur because mirrors and beam apertures have finite size.
Accessory losses stem from extra optical components and system imperfections.
Among these, geometric loss is one critical factor for resonator performance. From geometric optics view, geometric loss measures if light rays stay confined in cavity or escape after multiple round trips. When rays escape cavity boundaries, they cause big power losses and hurt laser efficiency.
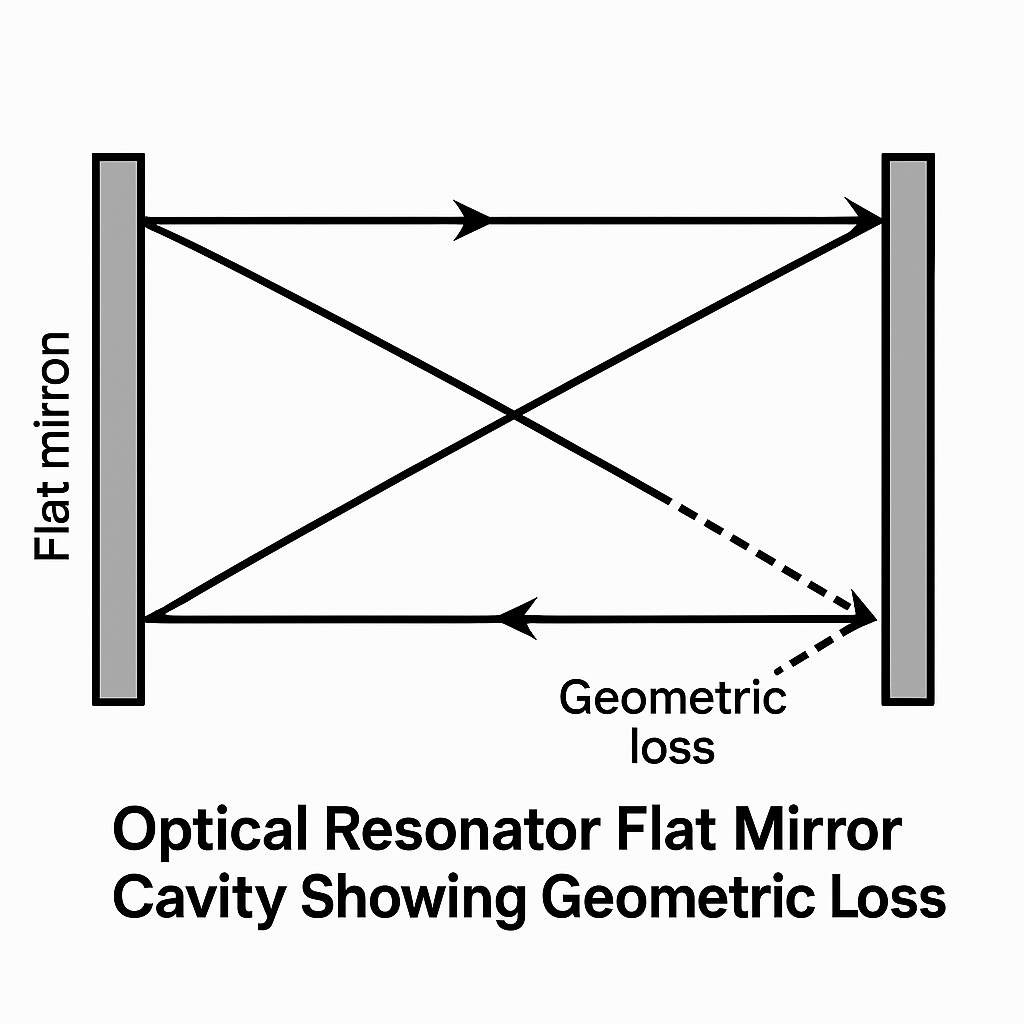
Fabry - Perot (F - P) cavity, with two parallel plane mirrors, is the most basic optical resonator design. In this setup, only light rays moving strictly perpendicular to cavity axis stay confined in resonator during multiple round trips. Any ray straying from this perpendicular path will escape cavity after limited reflections. This causes big geometric losses.
This geometric rule makes F - P cavities very sensitive to alignment parameters. Even small mirror parallelism errors can sharply raise geometric loss. Almost all light rays will escape cavity fast. The math relationship for this shows: for a plane - parallel resonator, stability parameter g₁g₂ equals 1. It sits right at boundary between stable and unstable operation.
F - P cavities’ sensitivity to alignment errors comes from their basic geometric properties. In a perfectly aligned system, rays must hit exactly perpendicular to avoid slowly drifting toward cavity edges. But real - world mirror flatness, parallelism, and mounting stability flaws make this ideal state hard to keep consistently.
Resonator instability happens when small cavity parameter changes cause sharp rises in geometric loss. This instability shows as fast drop in laser output power. It can even stop laser oscillation. For F - P cavities, instability comes from their marginal stability condition. The system works right at boundary between stable and unstable regimes.
When a resonator turns unstable, light rays no longer stay near optical axis during propagation. Instead, they keep diverging with each round trip until exceeding mirrors’ physical boundaries. This causes losses that grow exponentially. They quickly overcome gain from laser medium.
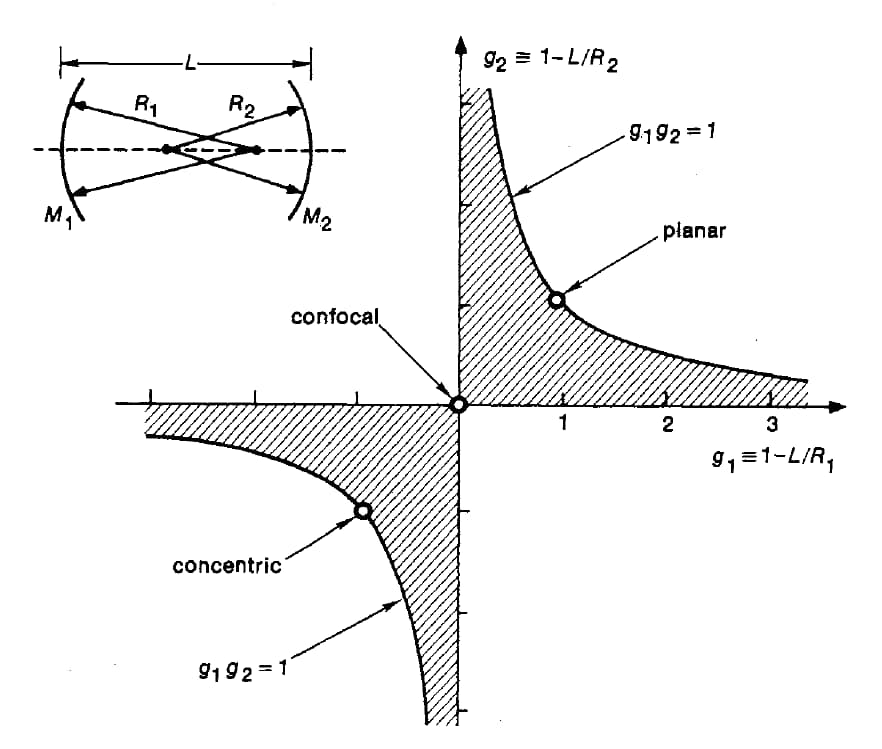
Stable resonator operation is a must for reliable laser performance. The stability condition for any two - mirror resonator is 0 ≤ g₁g₂ ≤ 1. Here, g₁ = 1 - L/R₁ and g₂ = 1 - L/R₂. L is cavity length. R₁, R₂ are mirror radii of curvature. This relationship gives a basic framework for designing stable optical resonators.
Coaxial spherical cavity is a better choice than F - P setup. It swaps flat mirrors for concave spherical mirrors. This design change brings much better stability than flat mirror systems. It lets paraxial rays (rays with small angles to optical axis) stay confined in resonator.
The big advantage of spherical mirrors is their focusing action. It counteracts light beams’ natural divergence. When designed right, curved mirrors’ focusing effect exactly balances beam diffraction. This creates stable resonator modes that keep their spatial profile after each round trip.
Several specific spherical mirror resonator setups have unique advantages:
Confocal resonators use two spherical mirrors with equal radii of curvature R. They’re separated by distance L = R. This setup puts both mirrors’ focal points at same spot. It creates stability parameter g₁g₂ = 0. Confocal design offers great mode confinement and good stability margins.
Concentric resonators use two spherical mirrors with radii R₁ = R₂ = L/2. Their centers of curvature match. This setup gives g₁g₂ = 1. It sits at stability boundary but has different mode characteristics than F - P cavities.
Practical benefits of spherical mirror resonators go beyond theory. Spherical surfaces are easier to make with high precision than perfectly flat mirrors. This makes them more cost - effective for many uses. Also, curved mirrors’ focusing properties enable better mode matching and less sensitivity to alignment errors.
Core differences between F - P and coaxial spherical cavities lead to distinct performance traits and best uses. F - P cavities, despite alignment sensitivity, work in simple interferometry and some laser diode setups. Their straightforward design and easy manufacturing give advantages.
Coaxial spherical cavities, especially confocal and near - confocal designs, shine in apps needing high stability and beam quality. These systems are often used in high - power laser systems, precision measurement instruments, and scientific research apps. Long - term stability and reproducible performance matter here.
Choosing between these setups often means trading complexity, cost, and performance needs. F - P cavities offer simplicity and lower manufacturing costs. Spherical mirror systems give better stability and beam quality but need more complex design and alignment.
The difference between F - P cavities and coaxial spherical cavities is a key choice in optical resonator design. It has big impacts on laser performance. F - P cavities, with their extreme alignment sensitivity and high geometric losses, are limited to apps where simplicity is more important than stability. In contrast, coaxial spherical cavities offer better stability via curved mirror design. They confine paraxial rays and cut geometric losses a lot.
Understanding these differences helps engineers and researchers make smart choices in laser system design. They balance performance needs against practical limits. As laser tech keeps evolving, the principles behind these basic resonator setups stay central to getting optimal system performance and reliability.
Ongoing development of advanced cavity designs — like hybrid setups and new mirror tech — builds on these basic ideas. It also tackles specific challenges of modern laser apps. Whether aiming for ultra - stable frequency references, high - power industrial systems, or compact portable devices, optical resonators’ basic physics keeps guiding innovation in laser tech.
Contact: Jason
Phone: +8613337332946
E-mail: [email protected]
Add: Hangzhou City, Zhejiang Province, China