Absorption Coefficient: How Materials Absorb Light

Absorption coefficient (α) measures how well an material absorbs light as it passes through. This property quantifies how fast light intensity fades on a material. It’s key on fields like optics, photonics, and materials science.

When light travels short distances (z) through an material, total absorption stays small. Absorbed power is roughly α×z×Pin (Pin is incident light power entering an material). Transmittance for short distances is about 1−α×z.

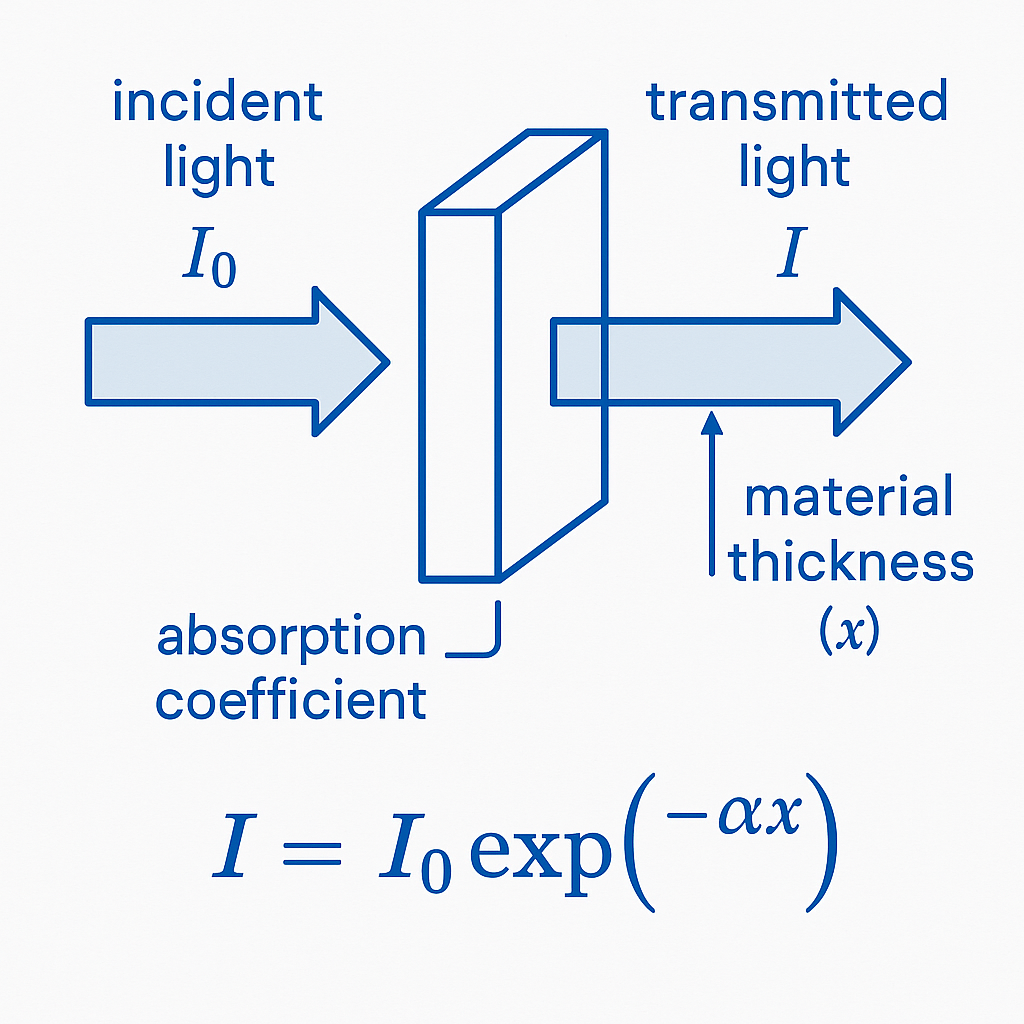
For longer distances, relationship turns exponential instead of linear. Longer propagation lengths use this equation: Transmittance = exp(-α×z). This works when scattering or reflection don’t affect light much. Higher α means faster light intensity drop.

Scientists and engineers use different absorption coefficients for an different apps.

Absorption coefficient usually measures decay of an optical power or intensity. But in some apps, researchers use an field amplitude absorption coefficient instead. This one measures how fast an electromagnetic field amplitude decreases—always half intensity coefficient. That’s because light intensity is square of an field amplitude.

In some fields, researchers use decimal absorption coefficient—standard one divided by an ln 10. With this, calculating absorption is easier—multiply an coefficient by optical path length.

Absorption coefficient ties directly to Beer-Lambert Law—absorbance goes up linearly with an concentration and path length. This lets scientists find unknown concentrations by measuring an light absorption.

When measuring an light attenuation, it’s important to tell different mechanisms apart. Exponential decay of an light intensity can come from absorption or reflection. Metals, for example, have strong exponential decay mostly from reflection, not an absorption. So scientists should check actual mechanism before calling it an “absorption coefficient.”

On materials with absorbing atoms or ions (like doped glass or crystals), absorption coefficient ties to microscopic properties. Specifically, it’s product of: - An doping density (atoms/ions per m³) - Absorption cross-section (m²) at the right wavelength. This links an material’s composition to its optical properties.

Different materials have an different absorption coefficients—changing how they interact with light.

Everyday Examples:

• Sunglasses: Darker tints have an higher absorption coefficients—blocking 40-80% of visible light (clear glass blocks an 2-5%).

• Water clarity: Clean ocean water has an low absorption coefficient (0.05-0.2 m⁻¹)—letting you see deep. Murky water has an higher (0.5-2.0 m⁻¹)—limiting visibility.

• Window tinting: Car tints go from an light (absorb an 10-30% of light) to dark (70-90%)—absorption coefficients 0.1-0.4 mm⁻¹ and 1.2-2.5 mm⁻¹.

• Fog: Dense fog has an absorption coefficients 20-50 m⁻¹—bad for driver visibility.

Technological Applications:

• Solar cells: Engineers design materials with an best absorption to make more electricity.

• Fiber optics: Less absorption lets an signals travel farther without loss.

• Medical imaging: Materials with an specific absorption improve contrast in diagnostics.

• Energy-efficient windows: Selective absorption of an wavelengths (transmitting others) saves energy in buildings.

Absorption coefficient gives an powerful math framework to understand how light interacts with matter. By measuring how fast an materials absorb light, it lets us explain an optical phenomena and design tech—from an sunglasses to photonic devices. Whether short-distance approximations or an long-distance exponential decay, absorption coefficient is essential on optics, materials science, and more.